Unit T Big Question Blog Post #4

4) Why do sine and cosine not have asymptotes, but the other four trig graphs do? Use unit circle ratios to explain.

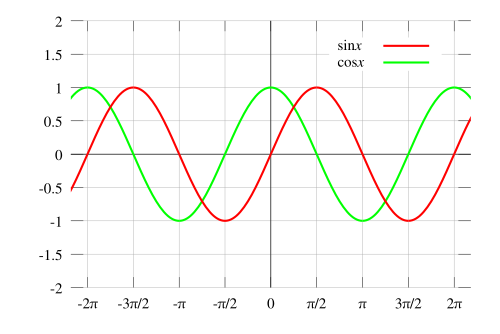
Sine and cosine do not have asymptotes because they are a wave when they are shown fully and they run forever on the x-axis. Also, cosine, in unit circle terms, is x/r and since r is always 1, cosine can never be undefined since r can never be zero, which is what makes a function undefined: when the denominator is zero. The same goes for sine. In unit circle terms, sine is y/r and since r is always 1, sine can never be undefined since r can never be zero, which is what is needed if you want to result in an asymptote: the denominator would have to be zero.



Secant, cosecant, tangent, and cotangent all have asymptotes of how x and y are zero in this case. Secant is 1/cos which is r/x. X can be any number and when it is zero, secant automatically becomes undefined and and asymptote is produced. The same goes for cosecant, which is r/y, except that when y is 0, cosecant becomes undefined and has an asymptote.
Tangent is sin/cos so when cosine is 0, it becomes undefined and produces an asymptote. Same goes for cotangent except that since cotangent is cos/sin, when sine is 0, cotangent becomes undefined and results in an asymptote. Overall, the theme is common: depending on the ratios from the functions, certain functions can never have asymptotes and others can.


Sources: http://en.wikibooks.org/wiki/Trigonometry/Graphs_of_Sine_and_Cosine_Functions
              http://en.wikipedia.org/wiki/File:Trigonometric_functions.svg

Unit T Big Question Blog Post #3

3) Why is a normal tangent graph uphill, but a normal cotangent graph downhill? Use the unit circle ratios to explain.






.
According to the unit circle, tangent is positive in the first and third quadrants which is why on the graph, tangent is above the x axis (positive) from 0 to pi/2 and pi to 3pi/2. Also, because the asymptotes for tangent are pi/2 and 3pi/2, it can explain why tangent is going towards those asymptotes meaning that because tangent stops being positive at the end of the first quadrant, it goes toward the asymptote to finish the cycle, and then starts going negative to start the second quadrant and so on. Tangent is in red and since red is going uphill, along with this explanation, that is why a normal tangent graph is uphill.

According to the unit circle, cotangent is positive in the first and third quadrants which is why on the graph, cotangent is above the x axis (positive) from 0 to pi/2 and pi to 3pi/2. Also, because the asymptotes for cotangent are 0 and pi, it can explain why cotangent is going towards those asymptotes, meaning that because cotangent stops being positive at the end of the first quadrant, it goes toward the asymptote to finish the cycle, and then starts going negative to start the second quadrant and so on. Cotangent is in blue and since blue is going downhill, along with this explanation, that is why a normal cotangent graph is downhill. The reason why it is downhill is also because it is the inverse of tangent so the direction is almost like a mirror image going in a different direction since they are reciprocals of each other.

Source:http://www.cartage.org.lb/en/themes/Sciences/Mathematics/Trigonometry/differentfund/different%20Functions%20.html

Unit T Big Question Blog Post #2

2) How do the graphs of sine and cosine relate to each of the others? Emphasize asymptotes in your response.

Well, sine and cosine don't have asymptotes but the rest of the trig functions do have asymptotes because at certain marks on the graph, sine can be 0 and cosine can be 0. These two functions relate to the others because all of the others have sine and/or cosine within them in one way or another. 

a) tangent. tangent is sine/cosine. When cosine is 0, that means that the trig function is undefined so there is an asymptote. Tangent's asymptotes are at pi/2 and 3pi/2.





 b) cotangent: cotangent is the inverse of tangent which means because tangent is sine/cosine, cotangent is cosine/sine. When sine is 0, there is an asymptote because of how the whole thing is made undefined at that particular moment. Tangent's asymptotes are at pi/2 and 3pi/2 so, to contrast, this means that cotangent's asymptotes are at 0 and pi. Using the graphs, notice how the asymptotes of the graph of y = tan(x) are the x-intercepts of the graph of y = cot(x). There are vertical asymptotes at each end of the cycle.  The asymptote that occurs at repeats every units



c) secant: secant is the inverse of cosine which means that it is 1/cosine and when cosine is 0 in this case, secant becomes undefined as a whole since it is the reciprocal of cosine. Anytime we have an undefined as our answer, we automatically know that there is going to be an asymptote. There are vertical asymptotes.  The asymptote that occurs at repeats every units


the pink is the parent graph of cosine and the brown is secant.

d) cosecant: cosecant is the reciprocal of sine making cosecant 1/sine. So, when sine is zero in this case, cosecant becomes undefined anytime sine is zero, thus resulting in an asymptote. The x-intercepts of y = sin x are the asymptotes for y = csc x. There are vertical asymptotes.  The asymptote that occurs at repeats every units






the brown is the cosecant graph and the blue is the parent graph of sine.

Excellent Source: http://www.regentsprep.org/Regents/math/algtrig/ATT7/othergraphs.htm

Unit T Big Question Blog Post #1

1) How do the trig graphs relate to the unit circle?
a) Period?-Why is the period for sine and cosine 2pi, whereas the period for tangent and cotangent is pi?

Well for sine and cosine, they have a period of 2pi because for both, their pattern of being positive or negative doesn't repeat until after four marks. On the unit circle, our quadrant angles (0,90,180,270, 360) in radians are 0, pi/2, pi, 3pi/2, and 2pi. Sine is positive in quadrant 1 and quadrant 2, thus meaning that it is negative in quadrant 3 and 4 which makes the pattern + + - -. Cosine is positive in quadrant 1 and quadrant 4, thus meaning that it is negative in quadrant 2 and 3 which makes thee pattern + - - +. As you can see, on the unit circle, the pattern for these two trig functions repeats only after one full revolution and since one revolution around the unit circle is 360 degrees, it has a period of 2pi. The same is on the graph except that the graph shows the unit circle in a different form on the x-axis. One period on a graph is like saying one revolution on the unit circle.



  

Source: http://www.upv.es/~rfuster/xpicture/functiongraphs.html




 However, tangent and cotangent have a period of pi because their pattern of being positive or negative only repeats after two marks, or half of a revolution. Tangent is positive in quadrant 1 and 3 and is negative in quadrant 2 and 4. Cotangent is the same. This means that the pattern is + - + -. According to the graph, you can notice after every two marks, tangent repeats.


Source: http://www.analyzemath.com/trigonometry/properties.html

b) Amplitude?-How does the fact that sine and cosine have amplitudes of one (and the other trig functions don't have amplitudes) relate to what we know about the unit circle?

First of all, sine and cosine have amplitudes of one because that is where the minimum and maximum points are, meaning that unlike the domain on a sine/cosine graph, the range is specific. The domain is all real numbers.Unlike sine and cosine, tangent and the rest of the trig functions have asymptotes, so when the functions are graphed in between the asymptotes, the vertex indicates where the function begins to go up to infinity or down to negative infinity.




Source: http://math.tutorvista.com/calculus/period-of-a-function.html


source: http://www.education.com/study-help/article/pre-calculus-help-other-trig-functions/
 

Student Video Unit S Concept 7

What is this video about?
This video is about solving equations with half angle formulas.These formulas include angles which are half of an angle on the unit circle. Depending on which quadrants we are in, sine, cosine, and tangent can all either be positive and/or negative.

What should the reader pay attention to?
The reader should pay attention to the formulas used and why anything squared is always positive. Also, when given radians, you must convert to degrees and find a coterminal angle within 360 degrees, if necessary, before moving on to do anything else.

Unit S Asessment #2: Half Angles and Sum and Difference Formulas

What is this picture about?
This picture is about half angles and the sum and difference formulas. The Unit Circle is essential in solving for the correct answers. It is also shows methods of simplification and in this case, we are using the sum formula.

What should the reader pay attention to?
The reader should pay attention to how similar the answers can be and how it is important to find the half angle to be able to use the correct formula.The viewer should also pay attention to how this is only an example of a sum formula and not a difference formula, meaning that if we were to use a difference formula, signs and variables would be tweaked (changed) just a bit.

Student Video: Unit S Concept 3

What is this video about?
This video is about using power-reducing formulas. Trigonometric identities and certain formulas are also used. Power reducing formulas, as explained in the video, allow us to lower the degree of a given function until we have simplified enough to the point where our highest degree (power) is one.

What should the reader pay attention to?
The reader should pay attention to how to break down our problem when we are simplifying to get the highest power to be 1. Also, knowing how to find a common denominator is essential for complete simplification. The viewer should also have an appropriate identities chart at hand which suits these type of problems, making them solvable.