Continuity is when something does not stop or is not interrupted by anything. A continuous function is predictable. It has no breaks in the graph, no holes, and no jumps. A function that is continuous can be drawn with a single, unbroken pencil stroke. In terms of limits, a function is continuous if the limit as x approaches a number of f(x) is equal to the height f(x) reaches at that point.
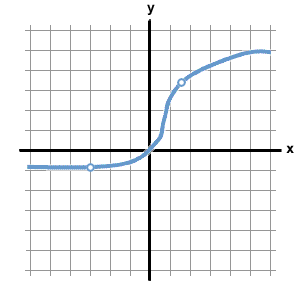
As you see above, this function goes on forever in both directions and is not interrupted by anything, meaning there are no jumps, holes, or breaks in the graph to disturb the continuity.
What is discontinuity?
Discontinuity is when something doesn't go on forever in both directions and is not continuous. There are two families of discontinuous functions. They are removable and non-removable discontinuities. The removable discontinuity is just called point discontinuity, also known as a hole. The non-removable discontinuities are jump discontinuity, oscillating behavior, and infinite discontinuity, which is known as unbounded behavior and occurs where there is a vertical asymptote.
Removable:
2) What is a limit? When does a limit exist? When does a limit not exist? What is the difference between a limit and a value?
A limit is the intended height of a function. The limit as x approaches 2 of f(x^2) is 4, for example. Even if there is a hole in the function, the limit still exists because the graph still intends to reach a certain height. A limit exists as long as you reach the same height from both the left and the right. The right hand limit is denoted with a +sign after the approached number and the left hand limit is denoted with a -sign after the approached number, in the notation of course. In order for a limit to exist, both the right hand limit and the left hand limit must be the same. If a graph doesn't break at a given value, a limit exists there.
Limits don't exist at the three non-removable discontinuities. Whenever a graph approaches different values from the left and the right, the limit does not exist.
The difference between a limit and a value is for example, in the photo above, the limit and the value are the same at a2 but are different at a3. At a3, the limit exists because it is the intended height of the function but the value doesn't because there is a hole. The limit is the intended height of the function while a value is the actual point.
3) How do we evaluate limits numerically, graphically, and algebraically?
We evaluate limits numerically by using a table. With the table, we find the intended heights of the whole function.
.JPG)
Lastly, we evaluate limits algebraically by using three different methods. These methods are the direct substitution method, the dividing out/factoring method, and the conjugate method (rationalizing method). The cool thing about these methods is that they go in order in a sort of last resort sort of way. If substitution doesn't work, we resort to the factoring method. If the factoring method doesn't work, we go to the rationalizing/conjugate method, which should always work. All of these methods are self-explanatory.
*Sometimes we will wan to find the limit of a function as x is getting bigger and bigger (approaching positive infinity) or smaller and smaller (approaching negative infinity). If we try to use direct substitution, we get to what is called indeterminate form. From there, we divide every term in the numerator and denominator by the highest power of x in the denominator to determine the limit. It's actually quite simple, really.
Cited Evidence:
