Student Video #1: Unit F Concept 10

  


What is this video about?
-This video covers a problem from Unit F Concept 10 which is finding all zeroes of a polynomial when the zeroes could be real and/or rational imaginary. The problem we chose was # 6 from the concept 6 and 10 extra problems from the unit F sss packet. In this video, we review the p's and q's, Descartes' rule of signs, using synthetic division, and factoring.

What does the viewer need to pay special attention to in order to understand the concept?
-Look at how many zeroes Descartes' rule says we are supposed to get and then look at how many zeroes we actually get.
-Notice how to use synthetic division again once you did it the first time.

Unit G Summary Question # 6 Holes

6. How do we find the appropriate place to plot a hole if the y-value is undefined when plugged into the original equation?

First, we have to factor the top and bottom of the rational function. If there are any common factors, then we cross them out. These common factors that we crossed out are our holes. To get the appropriate place, we would put zero as y because if it is undefined, then our denominator is zero and anything divided by zero is zero. We would plot the hole on the origin.

Unit G Summary Question #5 Asymptote Conditions

5. Describe the conditions in which a graph can cross through an asymptote.

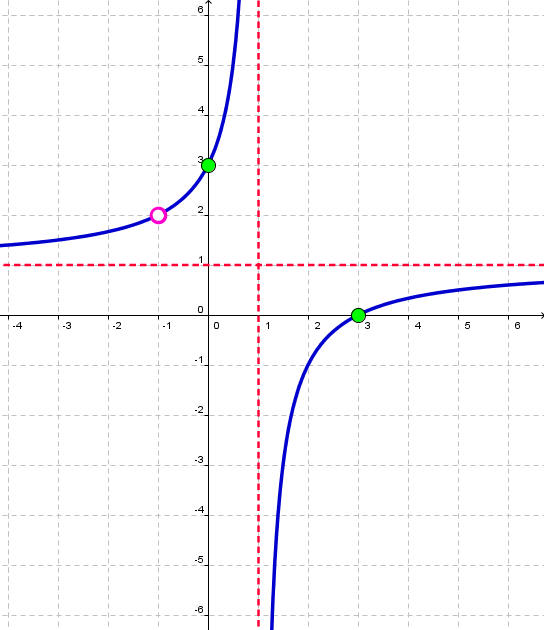
Graphs can sometimes cross through a horizontal asymptote, but only towards the middle of the graph; never towards the far left or far right. Graphs can sometimes cross through a slant asymptote towards the middle of the graph. Graphs can never ever cross through a vertical asymptote. In a sense, asymptotes are like the boundaries of graphs. The graphs get close to the asymptotes, but never really touch them. 

Unit G Summary Question #2 Limit Notation in Horizontal Asymptotes

 2. Describe what limit notation for horizontal asymptotes actually means.

Limit Notation for horizontal asymptotes means that as x approaches positive infinity, f of x approaches a number, and as x approaches negative infinity, f of x approaches a number. x never touches positive infinity, but it can get real close to it. The same goes for negative infinity. The number that f of x approaches is whatever y=. So if it were y=9, then the limit notation would be as x approaches positive infinity, f of x approaches 9 and as x approaches negative infinity, f of x also approaches 9.

Unit G Summary Question #7 Limit Notation

 7. Describe how to write limit notation for vertical asymptotes and what the notation means.

To write limit notation for vertical asymptotes, we have to factor the bottom and find the x intercepts. Then, those x intercepts become our vertical asymptotes. The notation for each intercept is the x intercept from the right and from the left. This means, say 2 for example, 2+ or 2- that 2 from the right and 2 from the left of the vertical asymptote, the graph goes up or down. Here, we put positive or negative infinity.

Unit G Summary Question # 4 Vertical Asymptotes and Holes

 4. What is the difference between a graph having a vertical asymptote and a graph having a hole?

The difference between a graph having a vertical asymptote and a graph having a hole is that for a vertical asymptote, we set the bottom equal to zero. In a hole, we set off the crossed off factors to zero. A vertical asymptote has limit notation and is x=#. A hole is plotted as a point (x,y). Also, a hole is  plotted with an open circle.

Unit G Summary Question #3 Slant Asymptotes

3. When does a graph have a slant asymptote? How do you find the equation of the slant asymptote?

A graph has a slant asymptote only when the degree of the top is one bigger than the degree on the bottom. We have to perform long division. When we do so, everything but our remainder is now the equation of the slant asymptote line. Graphs can sometimes cross through a slant asymptote towards the middle of the graph. The equation is always going to be y=mx+b.

Unit G Summary Question # 1 Horizontal Asymptotes

1. How do we know if a graph has a horizontal asymptote? What are the three options?

 We know if a graph has a horizontal asymptote when we compare the degrees of the numerator and the denominator. If there is a bigger degree on the bottom, then the asymptote is y=0. If the numerator and the denominator have the same degree, then the asymptote is the ratio of the coefficients. If there is a bigger degree on top, then there is no horizontal asymptotes. The equation is y=0. The limit notation is as x approaches positive infinity, f(x) approaches a number and as x approaches negative infinity, f(x) approaches a number.