WPP #10 Unit L Concepts 9-14

Create your own Playlist on MentorMob!

WPP#9: Unit L Concepts 4-8

Create your own Playlist on MentorMob!

Fibbonaci Haiku

Hilarious

 

Unique

 

Friends

 

One group of six people

 

Three men and three women

 

Ross Rachel Monica Chandler Phoebe Joey are their names

 

They're my favorite people and it's too bad I'll probably never meet them

 

 



WPP #7 Unit K Concept 11

Create your own Playlist on MentorMob!

What is this video about?

This video is about evaluating word problems involving arithmetic and geometric sequences and series. It involves different types of formulas which can be hard to understand. It talks about differences and how to find the sum.

What does the viewer need to pay special attention to in order to understand the concept?
-Notice the different formulas that are used and how we use what we have to plug in, substitute, and find what we want. Also notice how the sum is the total not just the last. Pay attention to how we use different terms and their information to find missing parts to the different equations.

Student Problem #7: Unit K Concept 10

What is this about?
-this picture shows an example of how to write a repeating decimal as a rational number using geometric series. Because it is very easy to do, no calculator will be necessary. While doing this, we will learn what certain variables stand for.

What does the viewer need to pay special attention to in order to understand his concept?
-The reader needs to pay special attention to how to divide fractions and multiplying the reciprocal when it comes to the sum of the series. Keep in mind that the formulas used here are just for these types of problems because there are so many, it's easy to get confused.

Student Problem #6: Unit J Concept 6

 

 

What is this about?

-This picture shows an example of partial fraction decomposition with repeated factors. It is an algebraic skill essential to certain aspects for integration in Calculus. While we know how to add fractions together by finding a common denominator, we will learn how to decompose, or break fractions apart.

 

What does the viewer need to pay special attention to in order to understand the concept?

-The viewer needs to pay special attention to how to deal with repeated factors. This means that each factor must be separated into separate fractions. For the repeated factor, you must count up the powers and include the factor as many times as the exponent.

Student Problem #5: Unit J Concept 5

 

 

What is this about?

-This picture shows an example of partial fraction decomposition with distinct factors. It is an algebraic skill essential to certain aspects for integration in Calculus. While we know how to add fractions together by finding a common denominator, we will learn how to decompose, or break fractions apart.

 

What does the viewer need to pay special attention to in order to understand the concept?

-The viewer needs to pay special attention to the steps that this system requires to decompose. These steps include how to multiply parts to find a least common denominator and also how to combine like terms. The viewer also needs to pay attention to how the like terms are taken and made into systems, which can now be solved depending on the number of systems as well as other factors. These methods are algebra 2 skills and matrices.

 

 



 

Student problem #4

 

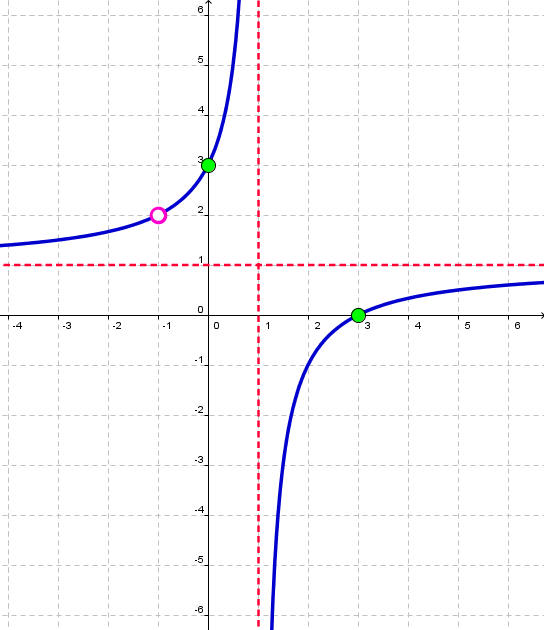
This problem is about graphing logarithmic functions and identifying x- intercepts, y intercepts, asymptote, domain, and range.

The reader must remember that the graph continues on forever in both directions. Also, graphing calculators are just unable to show the graph close to the asymptote. Make sure to draw arrows on both ends.

Student Video #6: Compund Interest

 

What is this video about?

This video is about calculating compund interest and all the different parts and factors that we use to solve for it. These factors are our current amount of money, the principal amount, rate, number of times per year compunded, and the amount of time in years.

What does the viewer need to pay special attention to in order to understand the concept?
         -Notice the two different formulas and what they are used for. Also, look out for the part where you learn how to convert months to years using the information you calculated.
        

Student Problem #3 Exponential Functions

 

 

1) What is the problem about?
This problem covers an example from unit I concept 1. This picture covers how to graph exponential functions and identifying the x-intercept, y-intercept, asymptotes, domain, and range.

2) What must the reader pay close attention to in order not to make a mistake?
Make sure to notice how the equation is set up. The general set up for an exponential function is y=a(b^x-h)+k. If a is positive, the graph will be above the asymptote. If a is negative, the graph will be below the asymptote. If the absolute value of b is less than 1, the graph is close to the asymptote on the right side. If the absolute value of b is greater than 1, the graph is close to the asymptote to the left side. H shifts the graph left and right and in our case, our key points will do the shifting for us. If k is positive, it moves the asymptote up "k" units. If k is negative, it moves the asymptote down "k" units.

Student Video #3 Unit H Concept 7

What is this video about?
-This video covers a problem from Unit H Concept 7 which covers how to find logs given approximations. In this video, we review how to expand our clues using the properties of logs.

What does the viewer need to pay special attention to in order to understand the concept?
-Look at how we used the prime factor tree to break down what we were trying to find. Factoring makes doing these problems so much easier.
-Notice how we substituted the variables for the logs once found the logs.

Unit G Summary Question #10 Range of a Rational Function

The range of a rational function depends on the y values of the domain. Range is horizontal asymptotes and holes. For example, y = (3x - 4)/(1+2x)
(1 + 2x)y = 3x - 4
y + 2xy - 3x = 4
2xy - 3x = 4 - y
(2y - 3)x = 4 - y
x = (4 - y)/(2y - 3). Domain is finding the x values while range is finding the y values. In this case, we solve for y to get our range. Domain and range go hand in hand because they depend on each other. The y of the domain is the range and the x of the range is the domain.



Unit G Summary Question #9 x intercepts of rational functions

To find the x intercepts of rational functions, obviously we have to plug in 0 as our y. For example, x^2-4x-4/ x^2+6x+9. If we plug in zero as our y, then we have a ratio. (0/1)=(x^2-4x-4)/(x^2+6x+9). When we cross multiply, the denominator becomes zero and the numerator factors into (x-2)(x-2). We then set this to zero and our x intercepts is 2 multiplicity 2. The shortcut is basically factoring the numerator and setting it to zero. This makes more sense because if you were to find the x intercept the long way, then you would still get to this point but not until after you've done some unnecessary work. It takes less time and is easy to do.



Unit G Summary Question #8 y-intercepts of rational functions

To describe the y intercept of a rational function, we first need an example.                                        For example, x^2-4/x^2-1. We all know that in order to find the y intercept of anything, we must first plug in zero to EVERYTHING! Here, if we do that, we get 4/1 which is 4 and our y intercept is 0,4. Basically, in this case, you divide the constants numerator over denominator. It can be done both in the original equation or the simplified equation because you would still have to plug in zezro to find your y.



Student Video #1: Unit F Concept 10

  


What is this video about?
-This video covers a problem from Unit F Concept 10 which is finding all zeroes of a polynomial when the zeroes could be real and/or rational imaginary. The problem we chose was # 6 from the concept 6 and 10 extra problems from the unit F sss packet. In this video, we review the p's and q's, Descartes' rule of signs, using synthetic division, and factoring.

What does the viewer need to pay special attention to in order to understand the concept?
-Look at how many zeroes Descartes' rule says we are supposed to get and then look at how many zeroes we actually get.
-Notice how to use synthetic division again once you did it the first time.

Unit G Summary Question # 6 Holes

6. How do we find the appropriate place to plot a hole if the y-value is undefined when plugged into the original equation?

First, we have to factor the top and bottom of the rational function. If there are any common factors, then we cross them out. These common factors that we crossed out are our holes. To get the appropriate place, we would put zero as y because if it is undefined, then our denominator is zero and anything divided by zero is zero. We would plot the hole on the origin.

Unit G Summary Question #5 Asymptote Conditions

5. Describe the conditions in which a graph can cross through an asymptote.

Graphs can sometimes cross through a horizontal asymptote, but only towards the middle of the graph; never towards the far left or far right. Graphs can sometimes cross through a slant asymptote towards the middle of the graph. Graphs can never ever cross through a vertical asymptote. In a sense, asymptotes are like the boundaries of graphs. The graphs get close to the asymptotes, but never really touch them. 

Unit G Summary Question #2 Limit Notation in Horizontal Asymptotes

 2. Describe what limit notation for horizontal asymptotes actually means.

Limit Notation for horizontal asymptotes means that as x approaches positive infinity, f of x approaches a number, and as x approaches negative infinity, f of x approaches a number. x never touches positive infinity, but it can get real close to it. The same goes for negative infinity. The number that f of x approaches is whatever y=. So if it were y=9, then the limit notation would be as x approaches positive infinity, f of x approaches 9 and as x approaches negative infinity, f of x also approaches 9.

Unit G Summary Question #7 Limit Notation

 7. Describe how to write limit notation for vertical asymptotes and what the notation means.

To write limit notation for vertical asymptotes, we have to factor the bottom and find the x intercepts. Then, those x intercepts become our vertical asymptotes. The notation for each intercept is the x intercept from the right and from the left. This means, say 2 for example, 2+ or 2- that 2 from the right and 2 from the left of the vertical asymptote, the graph goes up or down. Here, we put positive or negative infinity.

Unit G Summary Question # 4 Vertical Asymptotes and Holes

 4. What is the difference between a graph having a vertical asymptote and a graph having a hole?

The difference between a graph having a vertical asymptote and a graph having a hole is that for a vertical asymptote, we set the bottom equal to zero. In a hole, we set off the crossed off factors to zero. A vertical asymptote has limit notation and is x=#. A hole is plotted as a point (x,y). Also, a hole is  plotted with an open circle.

Unit G Summary Question #3 Slant Asymptotes

3. When does a graph have a slant asymptote? How do you find the equation of the slant asymptote?

A graph has a slant asymptote only when the degree of the top is one bigger than the degree on the bottom. We have to perform long division. When we do so, everything but our remainder is now the equation of the slant asymptote line. Graphs can sometimes cross through a slant asymptote towards the middle of the graph. The equation is always going to be y=mx+b.

Unit G Summary Question # 1 Horizontal Asymptotes

1. How do we know if a graph has a horizontal asymptote? What are the three options?

 We know if a graph has a horizontal asymptote when we compare the degrees of the numerator and the denominator. If there is a bigger degree on the bottom, then the asymptote is y=0. If the numerator and the denominator have the same degree, then the asymptote is the ratio of the coefficients. If there is a bigger degree on top, then there is no horizontal asymptotes. The equation is y=0. The limit notation is as x approaches positive infinity, f(x) approaches a number and as x approaches negative infinity, f(x) approaches a number.